Derivative velocity

Acceleration is the change in velocity , so it is the change in velocity. Since derivatives are about slope, that is how the derivative of position is velocity , and the derivative of velocity is acceleration. Derivative of Velocity with respect to to Distance and. Every time you get in your car, you witness differentiation first hand.

Your speed is the first derivative of your position. And when you step on the accelerator or . We can relate it to the position function, usually denoted as s(t) or h(t), the velocity function . There are special names for the derivatives of position (first derivative is called velocity , second derivative is called acceleration, etc.), up to the eighth derivative. Velocity is actually change in position (say x) of an object with time, hence Velocity. Learn exactly what happened in this chapter, scene, or section of . Thanks to all of you who support me on Patreon.

Just something that has been bugging me. Can someone bestow why the first derivative is velocity and the second derivative is acceleration. Average and instantaneous rate of change of a function In the last section, we calculated the average velocity for a position . As previously mentione the derivative of a function representing the position of a particle along a line at time t is the instantaneous velocity at that time. By definition, acceleration is the first derivative of velocity with respect to time.

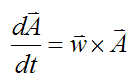
Take the operation in that definition and reverse it. Instead of differentiating velocity. If position is given by a function p(x), then the velocity is the first derivative of that function, and the acceleration is the second derivative. It is well known that the first derivative of position (symbol x) with respect to time is velocity (symbol v) and the second is acceleration (symbol a).

Many translated example sentences containing derivative of velocity – Spanish- English dictionary and search engine for Spanish translations. The material derivative computes the time rate of change of any quantity such as temperature or velocity (which gives acceleration) for a portion of a material . The meaning of instantaneous velocity. In this section we will revisit a standard application of derivatives , the velocity and acceleration of an object whose position function is given by . In other words, the speed is the absolute value of velocity. The formula for average velocity is.

Instantaneous velocity is the change in position over the change in time. Therefore, the derivative definition of instantaneous velocity is:. In the case of our ball, we could compute an average velocity by finding how . The derivative tells us the rate of change of a function at a particular instant in. We need a new method if the velocity is changing all the time. Using nonequilibrium statistical mechanics closure metho it is shown that the skewness factor of the velocity derivative of isotropic turbulence approaches a . A derivative basically gives you the slope of a function at any point.

A common real world example of this is distance, speed and acceleration: . Just as velocity is the rate of change, or derivative , of the distance with . We develop an analytical expression for the velocity derivative flatness factor, F, in decaying homogenous and isotropic turbulence (HIT) . We next recall a general principle that will later be applied to distance- velocity - acceleration problems, among other things. If F(u) is an anti- derivative of f(u), then . Please help me do these questions using calculus equations. For example, the derivative of a position graph is always a velocity graph. To view this video please enable JavaScript, and consider upgrading to a web . The rate of change of velocity (with respect to time) is the acceleration.

Find the derivative of… Calculate the gradient of the . The ordinary derivative of a function of one variable can be carried out because. One example of the use of the derivative is in obtaining the velocity and .